Effectiveness of Scientific Calculator in Learning
What is the Effectiveness of Scientific Calculator?

Easily Integrating Real-Life Problems into Learning
By using a scientific calculator, complex real-life numbers can be calculated easily. This enables the handling of various real-world problems in learning, allowing learners to deeply understand the connection between academic subjects and daily life. As a result, it can spark learners' curiosity about the subjects.
Support Learning Focused on the Thinking Process
Scientific calculators help explore mathematical concepts and reduce calculation time, allowing learners to focus on the thinking process in their learning. As a result, they can develop valuable skills needed in today’s world such as critical thinking and problem-solving skills.
Examples of How to Use
Scientific Calculator Effectively
1 Enabling Complex Calculations Allows Real-World Applications
Q. Calculate the actual height of a tower.
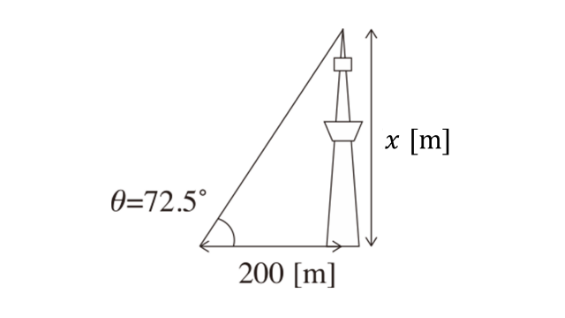
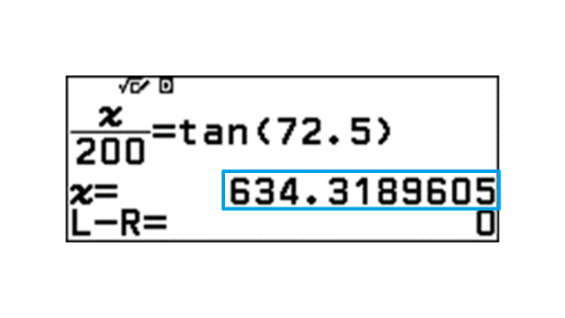
The tower height is 634m.
Q. Calculate the probability of 2 out of x people having the same birthday.




With 30 people, the probability reaches 70%.
2 Instant Statistical Calculations to Enhance Focus on Analysis
Q. Simulate tossing three coins 250 times and analyze it.


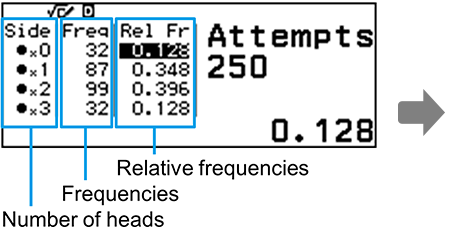
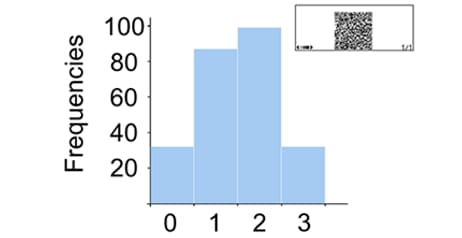
Note: To view this histogram, you need to create QR code and scan it with your smartphone.
The probabilities are confirmed to be close to the theoretical values.
Q. Calculate the mean and variance of datasets (1) and (2), and also plot the scatter diagram.

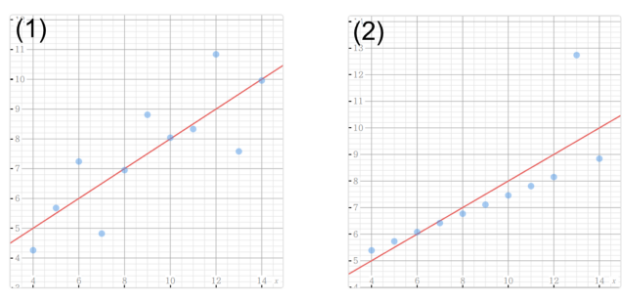
The means and variances of (1) and (2) are almost the same, but the data trends are completely different.
3 Support Exploration Learning
Q. Consider the deposit amounts of two savings accounts with different interest rates after x years.





The amounts reverse in 18 years as the value of x increases.
Q. Explore whether the definition of Euler's number (e) is really correct.
The definition of Euler's number (e)

Mathematical exploration can be performed by inputting various values for x.

Substituting a large number for x, Euler's Number (e) appears.
4 Trigger Further Questions and Support Problem Solving
Q. Solve the simultaneous equations.
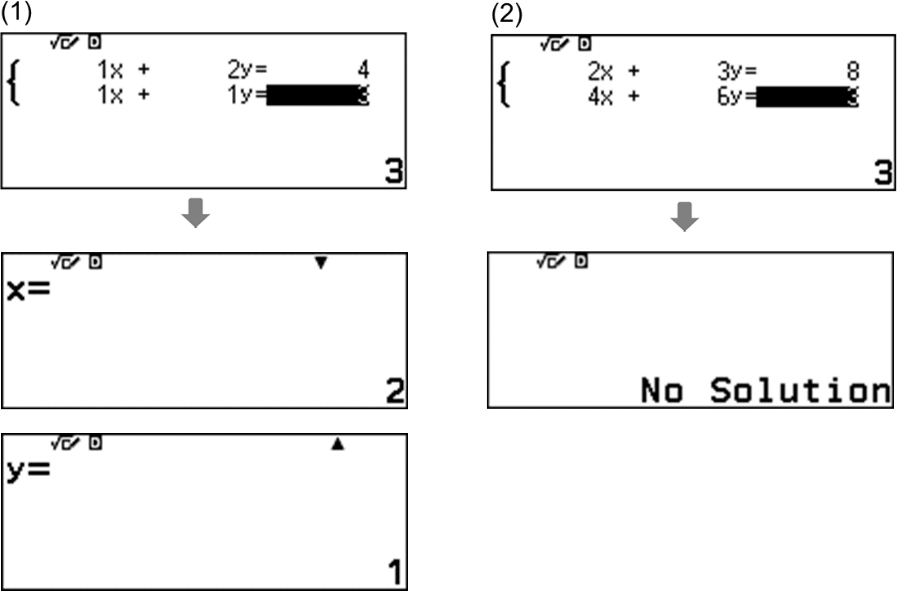

Why do the equations in (2) have No Solution?
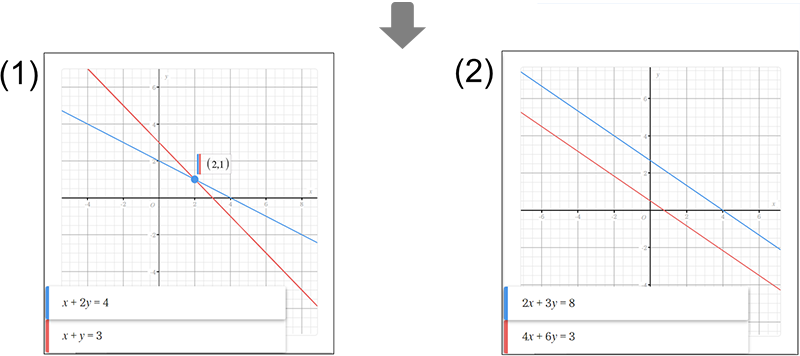

The two graphs in (2) are parallel and have no intersection, which shows that there is No Solution.
Q. Give the following values as decimals.


How does the value change as the number of square root signs increases?
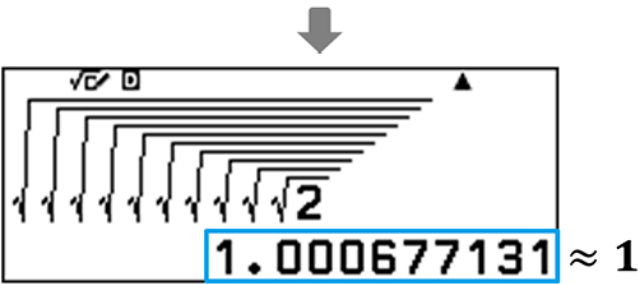

The value approaches 1 as square root signs increase.

You can download the teaching materials using a scientific calculator here.
How Scientific Calculators Have a Positive Impact on Student's Thinking Skills