ประสิทธิภาพของเครื่องคำนวณวิทยาศาสตร์ที่มีต่อการเรียน
เครื่องคำนวณวิทยาศาสตร์
มีประสิทธิภาพต่อการเรียนมากน้อยเพียงใด

สามารถบูรณาการสถานการณ์ปัญหาชีวิตจริงให้เข้ากับการเรียน
ได้อย่างง่ายดาย
การใช้เครื่องคำนวณวิทยาศาสตร์ ทำให้สามารถคำนวณตัวเลขที่ซับซ้อนได้ง่ายขึ้น ซึ่งจะช่วยผู้เรียนมีเวลาในการวิเคราะห์ สามารถเรียนรู้และเข้าใจสถานการณ์ปัญหา
ได้ลึกซึ้ง ผู้เรียนจะสามารถเชื่อมโยงปัญหาต่าง ๆ ในโลกความเป็นจริงในชีวิตประจำวันโดยใช้การคำนวณ ผลลัพธ์ที่ได้ คือผู้เรียนจะมีความกระตือรือร้นในการเรียนมากขึ้น
สนับสนุนการเรียนรู้โดยมุ่งเน้นที่กระบวนการคิด
เครื่องคำนวณวิทยาศาตร์ช่วยลดเวลาในการคำนวณ ทำให้ผู้เรียนสามารถมีเวลามุ่งเน้นไปที่กระบวนการคิดวิเคราะห์ในการเรียนรู้มากขึ้น ส่งผลให้นักเรียนมีทักษะที่จำเป็น
ต่อความต้องการในตลาดแรงงานปัจจุบัน เช่น ทักษะการคิดเชิงวิพากษ์และการแก้ปัญหา
ตัวอย่างการใช้งาน
เครื่องคำนวณวิทยาศาสตร์ให้มีประสิทธิภาพ
1 ช่วยการคำนวณที่ซับซ้อน ส่งผลดีต่อการใช้งานในสถานการณ์ปัญหาชีวิตจริง
ตัวอย่าง การคำนวณความสูงของหอคอย
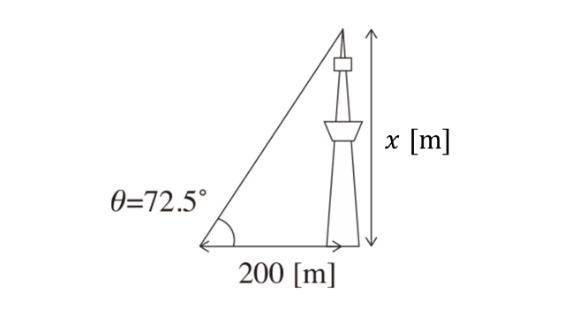
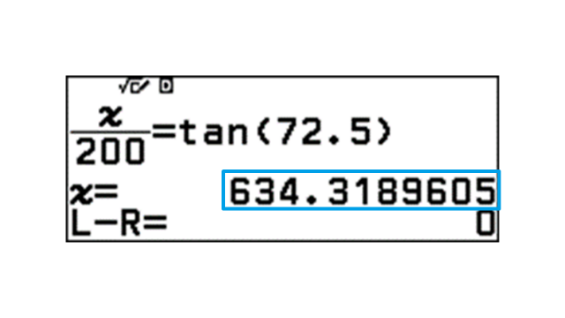
ความสูงของหอคอยคือ 634 เมตร
ตัวอย่าง จงคำนวณความน่าจะเป็นของเหตุการณ์ที่คน 2 คน จะมีวันเกิดวันเดียวกัน




หากพิจารณา N = 30 คน จะได้ว่าความน่าจะเป็นมีค่าประมาณ 0.71 หรือ 71%
2 การคำนวณสถิติ เพื่อเสริมสร้างการคิดวิเคราะห์
ตัวอย่าง ให้ทดลองโยนเหรียญสามเหรียญ 250 ครั้งและทำการวิเคราะห์ผลลัพธ์

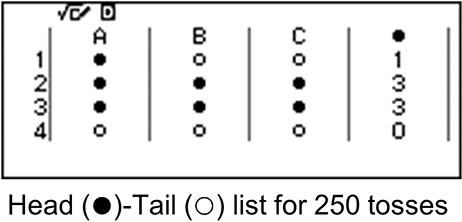
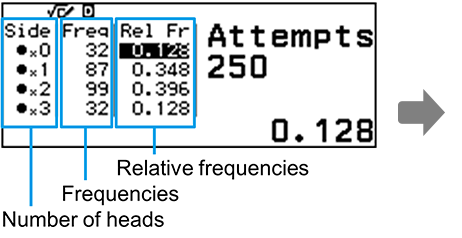
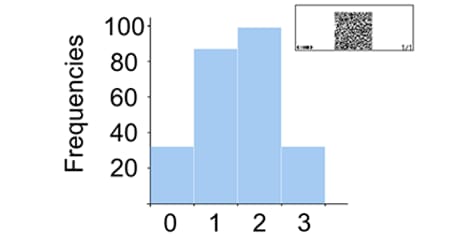
หมายเหตุ: เพื่อดูฮิสโตแกรมนี้ คุณต้องสร้างคิวอาร์โค้ดและสแกนก้วยสมาร์ทโฟน
จะพบว่าความเป็นไปได้ มีค่าใกล้เคียงกับค่าในทางทฤษฎี
ตัวอย่าง จงคำนวณค่าเฉลี่ยและความแปรปรวนของชุดข้อมูล (1) และ (2) และวาดกราฟแสดงกระจายของข้อมูล

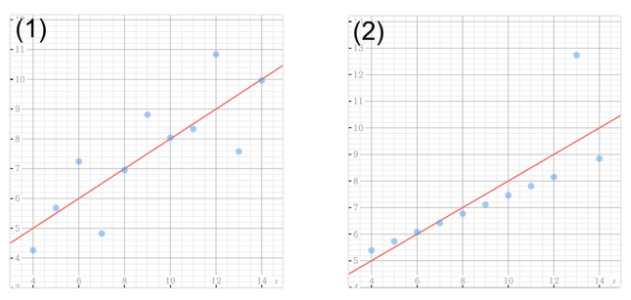
ค่าเฉลี่ยและความแปรปรวนของชุดข้อมูล (1) และ (2) มีความคล้ายกัน แต่แนวโน้มของข้อมูลต่างกันโดยสิ้นเชิง
3 สนับสนุนการเรียนรู้แบบสืบเสาะ
ตัวอย่าง พิจารณาจำนวนเงินฝากและอัตราดอกเบี้ย ของสองบัญชีที่ต่างกัน
หลังจากผ่านไป x ปี


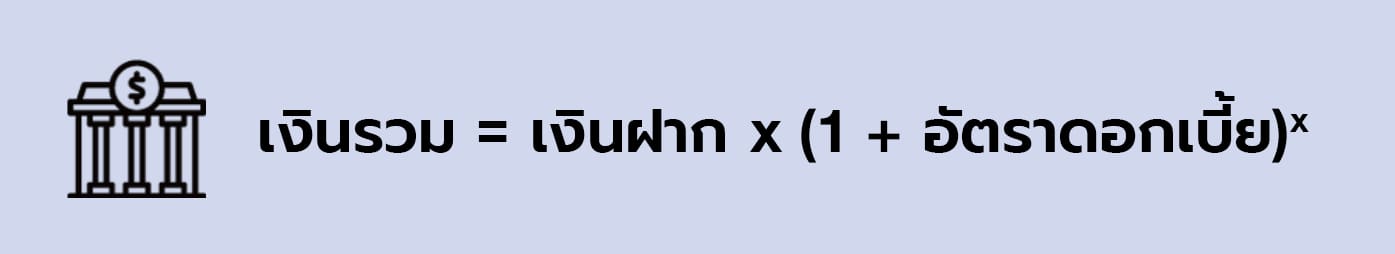

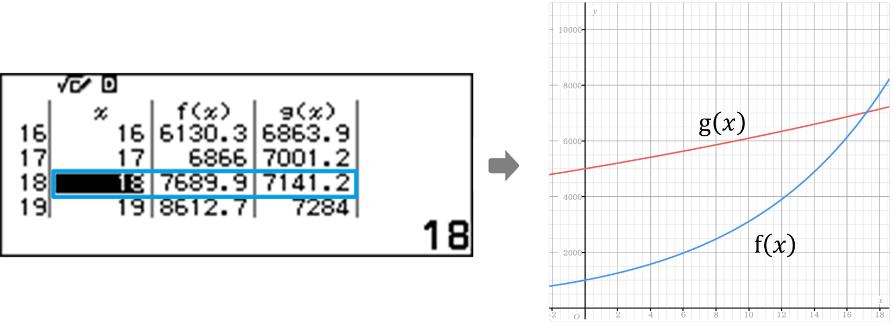
จำนวนเงินของทั้งสองบัญชีจะเริ่มมีความแตกต่างกันชัดเจนมากขึ้น เมื่อเวลาผ่านไป 18 ปี
ตัวอย่าง จงตรวจสอบนิยามจำนวนของออยเลอร์ (e)
นิยามจำนวนของออยเลอร์ (e)
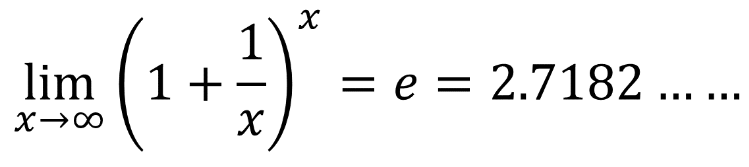
การตรวจสอบและสำรวจทางคณิตศาสตร์สามารถทำได้โดยการแทนค่า x เป็นจำนวนต่าง ๆ
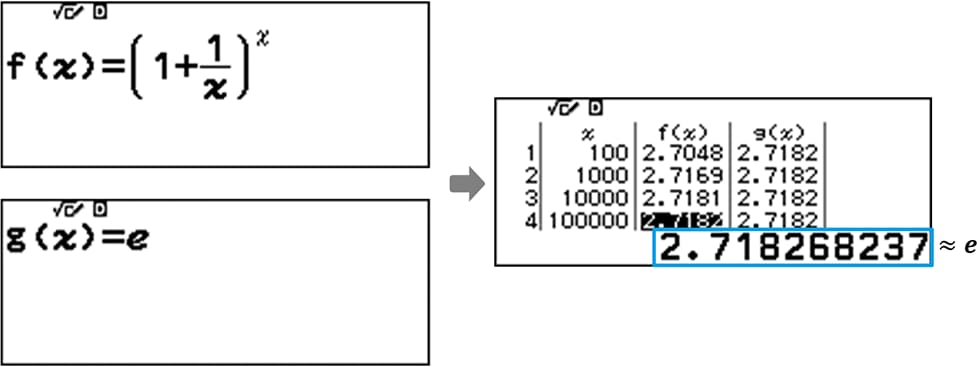
เมื่อแทนค่าจำนวนมาก ๆ ลงใน x ค่าจะเข้าใกล้จำนวนของออยเลอร์ (e) มากยิ่งขึ้น
4 สร้างคำถามต่อยอดและสนับสนุนการแก้ไขปัญหา
ตัวอย่าง จงแก้ระบบสมการ x + 2y = 4
x + y = 3
และ 2x + 3y = 8
4x + 6y = 3
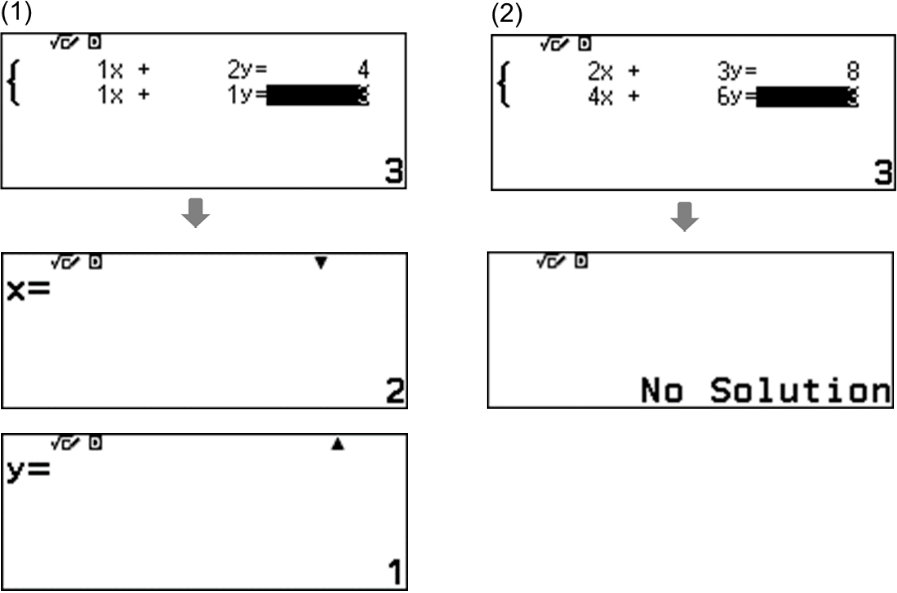

เพราะเหตุใด สมการ (2) จึงไม่มีคำตอบ
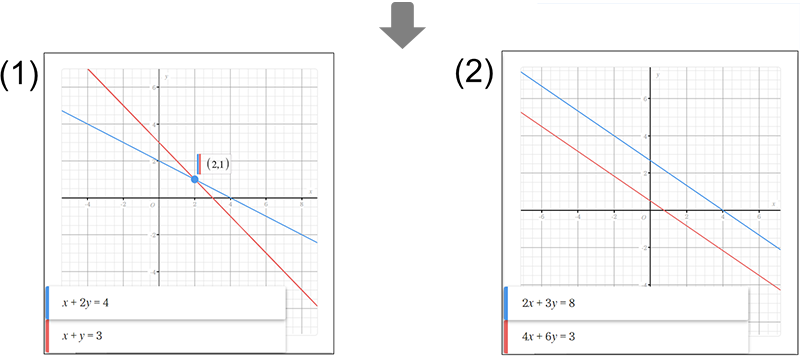

กราฟในสมการ (2) ขนานกันและไม่มีการตัดกัน ซึ่งแสดงให้เห็นว่าไม่มีคำตอบ
ตัวอย่าง จงเปลี่ยนจำนวนต่อไปนี้ให้อยู่ในรูปทศนิยม


ค่าของจำนวนมีการเปลี่ยนแปลงอย่างไรเมื่อใส่จำนวนรากที่สองเพิ่มขึ้น
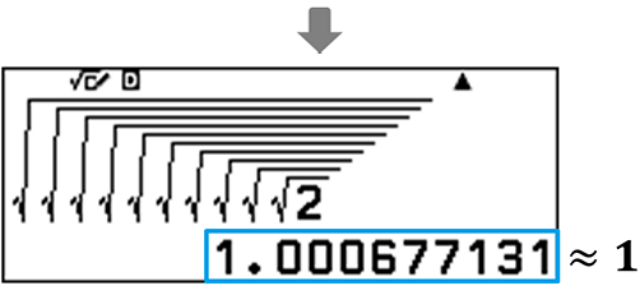

ค่าจะเข้าใกล้ 1 เมื่อใส่จำนวนรากที่สองเพิ่มขึ้น

คุณสามารถดาวน์โหลดสื่อการสอน
โดยใช้เครื่องคำนวณวิทยาศาสตร์ได้ที่นี่
เครื่องคำนวณวิทยาศาสตร์ส่งผลดีต่อทักษะการคิดของนักเรียนได้อย่างไร